Le carré magique

Le carré magique est composé d’un nombre de cases égal au carré du nombre choisi (l’ordre).
Ainsi, le carré d’ordre 3 est composé de 9 cases correspondant aux 9 chiffres (3²) de notre système décimal. La caractéristique du carré magique est de faire apparaitre un nombre « magique » égal au total des chiffres figurant en l’espèce sur chacune des 8 lignes, colonnes et diagonales le constituant.

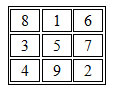
Ici ce nombre est aisé à calculer puisque le total des nombres des 3 colonnes (ou lignes) du carré (1+2+3…….+8+9) est égal à 45 soit 15 par colonne qui est donc le nombre magique. Les 8 combinaisons possibles (1+5+9, 1+6+8, 2+4+9, 2+5+8….) font apparaître 4 occurrences du chiffre 5, 3 pour chaque chiffre pair et 2 pour les chiffres impairs autres que 5.

Ces fréquences guident la façon de répartir les chiffres dans le carré magique; ainsi la case du centre se rencontre à 4 reprises puisque milieu des lignes, colonnes et diagonales. Cette occurrence commande donc d’y placer le chiffre 5. Par symétrie de raisonnement, chaque coin du carré intervient 1 fois en tant que ligne, colonne ou diagonale soit à 3 reprises, induisant l’emplacement des chiffres pairs (cf supra) : il ne reste plus alors qu’à compléter les cases vides avec les 4 autres chiffres impairs.

Exemple :

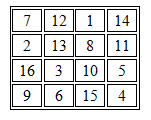
Dans Mélancholia, le peintre Albrecht Dürer a peint un carré magique d’ordre 4, réussissant à y intégrer la date de son tableau (1514).

On trouve aussi un carré d’ordre 4 dans le temple de Khajuraho en Inde du nord, réputé pour ses sculptures érotiques, les Mithuna. Ce carré dénommé  » Chautisa Yantra  » qui daterait du 10ème siècle après J-C. a pour caractéristique impressionnante qu’à l’intérieur, les 4 cases de chaque petit carré forment aussi la somme magique de 34: